线段树完全版关键词：延迟加载、懒标记Lazy Tag

单点更新的情况比较简单。请看 线段树基础版

下面说说区间更新的情况。

场景是这样的，还是刚刚的数，求区间的和。

准备工作

1
2
3
4
//rt:root
#define lson rt<<1
#define rson rt<<1|1
#define len (r-l+1) //(l,r)区间的长度

这次是区间更新，我们要用到区间的长度

建树

build和pushUp不变。我们把树建立好打印一下：

[1]:36 [2]:26 [3]:10 [4]:15 [5]:11 [6]:10 [7]:0 [8]:6 [9]:9 [10]:5 [11]:6 [12]:8 [13]:2 [14]:0

image-20181128195405878

pushDown 重点

延迟加载、懒标记思想：

假设现在要把区间【2,6】里5个数全加10，求总和。会数学的都知道，一共加了50，总和变成86。就是说对一段区间的统一操作，不需要对区间里的单个点进行改动。

只改动他们的老祖宗，并在他们的祖宗上做一个标记。以后啥事需要用到儿子了，一看父亲上有标记，就知道这个儿子还需要被更新。

下面的代码就是根据父亲rt，和对应的区间长度l，往下pushDown懒标记。

1
2
3
4
5
6
7
8
9
10
11
void pushDown(int rt,int len){//
    if(lazy[rt]){//这个点有lazyTag才往下下发lazyTag
      						//lazyTag里存的值是"要延迟加载的"值，例子就是10
        lazy[lson]+=lazy[rt];
        lazy[rson]+=lazy[rt];

        tree[lson]+=lazy[rt]*(len-len/2);//这里要注意
        tree[rson]+=lazy[rt]*(len/2);
        lazy[rt]=0;//清除父亲的标记
    }
}

注意第6行：举个例子来说明，rt代表的区间[1,7]，长度l为7，7/2=3.

而[1,7]的左右儿子是[1,4]和[5,7]这两个。左儿子长度为4,右儿子长度为3。

第6行那么写，就是要处理区间长度为奇数的情况，由于是完全二叉树，rt的左儿子代表的区间一定更长。

更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void update(int L,int R,int addVal,int l,int r,int rt){
    cout<<__func__<<l<<','<<r<<','<<rt<<'\n';
    //(l,r)就是根节点rt所代表的区间。
    //[L,R]是要更新的区间。
    if(L<=l&&R>=r){//(l,r)在[L,R]里
        tree[rt]+= len*addVal;//那就只更新rt，不用往下更新了。
        lazy[rt]+= addVal; //但必须做好lazy标记用于pushDown。标记的值就是要加的数。
        return;
    }
    //如果区间不能涵盖:
    pushDown(rt,r-l+1);//下放懒标记。防止以前有过改动儿子没加载
    int m = (l+r)>>1;
    if(L<=m)
        update(L,R,addVal,l,m,lson);
    if(R>m)
        update(L,R,addVal,m+1,r,rson);
    pushUp(rt);
}

我们还是通过例子看看程序是怎么执行的：

1
update(2,6,10,1,7,1);//2到6全加10

打印一下：

1
2
3
4
5
6
7
8
update1,7,1
update1,4,2
update1,2,4
update2,2,9
update3,4,5
update5,7,3
update5,6,6
[0]:0 [1]:86 [2]:56 [3]:30 [4]:25 [5]:31 [6]:30 [7]:0 [8]:6 [9]:19 [10]:5 [11]:6 [12]:8 [13]:2 [14]:0 [15]:0

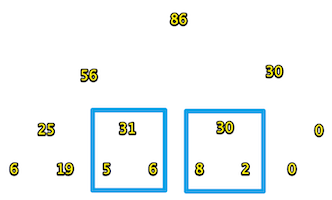
画出图：image-20181128211645919

可以看到，框里的数，5、6、8、2虽然没有被更新，但是他们的父亲却是正确的值。

查询

下面我们通过查询，来看一下lazyTag到底啥时候排上用场。

现在我们查询区间(3,5)这三个数的和，应该是49。

其中，区间(3,4)里的两个数虽然是5、6，但是他们的和31是正确的。

但是第4个数8就不对了，应该是18才对。

看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int query(int L,int R,int l,int r, int rt){//[L,R]是要查询的区间
    cout<<__func__<<" ["<<L<<','<<R<<"] ("<<l<<','<<r<<") "<<rt<<'\n';
    if(L<=l&&R>=r){//如果[L,R]里有(l,r)区间，直接返回对应的根节点
        return tree[rt];
    }
    pushDown(rt,len);//下放标记派上用场了
    int m = (l+r)>>1;
    int sum = 0;
    if(L<=m){
        sum += query(L,R,l,m,lson);
    }
    if(R>=m+1){
        sum += query(L,R,m+1,r,rson);
    }
    return sum;
}

输出结果：

1
2
3
4
5
6
7
8
query [3,5] (1,7) 1
query [3,5] (1,4) 2
query [3,5] (3,4) 5
query [3,5] (5,7) 3
query [3,5] (5,6) 6
pushDown rt:6 len:2
query [3,5] (5,5) 12
49

如我们所愿，

第5行，查询区间(5，6)，6不属于[3,5]，

往下执行到了pushDown(6),第6行输出了pushDown rt:6 len:2。

这时候我们如果再打印一下，就会发现，30的两个孩子8和2已经全部完成了延迟加载，成了18和12~

[1]:76 [2]:46 [3]:30 [4]:15 [5]:31 [6]:30 [7]:0 [8]:6 [9]:9 [10]:5 [11]:6 [12]:18 [13]:12 [14]:0

线段树完全版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
//线段树 求解区间最值问题
#include <iostream>
#include <vector>
#include "../Vt.h"
//rt:root
#define lson rt<<1
#define rson rt<<1|1
#define len (r-l+1)

using namespace std;

vector<int> vt{6,9,5,6,8,2,0};
int i = 0;
vector<int> tree(16);
vector<int> lazy(16);

void pushUp(int rt){
    tree[rt] = tree[lson]+tree[rson];
}

void build(int l,int r,int rt){
    if(l==r)//是叶节点，存数
    {
        tree[rt] = vt[i++];
        return;
    }
    int m = (l+r)>>1;
    build(l,m,lson);
    build(m+1,r,rson);
    pushUp(rt);
}

void pushDown(int rt,int l){
    if(lazy[rt]){//这个点有lazyTag才往下下发lazyTag
        cout<<__func__<<" rt:"<<rt<<" len:"<<l<<'\n';
        lazy[lson]+=lazy[rt];
        lazy[rson]+=lazy[rt];

        tree[lson]+=lazy[rt]*(l-l/2);//这里要注意
        tree[rson]+=lazy[rt]*(l/2);
        lazy[rt]=0;
    }
}

void update(int L,int R,int addVal,int l,int r,int rt){
    cout<<__func__<<l<<','<<r<<','<<rt<<'\n';
    //(l,r)就是根节点rt所代表的区间。
    //[L,R]是要更新的区间。
    if(L<=l&&R>=r){//(l,r)在[L,R]里
        tree[rt]+= len*addVal;//那就只更新rt，不用往下更新了。
        lazy[rt]+= addVal; //但必须做好lazy标记用于pushDown。标记的值就是要加的数。
        return;
    }
    //如果区间不能涵盖:
    pushDown(rt,r-l+1);//下放懒标记。防止以前有过改动儿子没加载
    int m = (l+r)>>1;
    if(L<=m)
        update(L,R,addVal,l,m,lson);
    if(R>=m+1)
        update(L,R,addVal,m+1,r,rson);
    pushUp(rt);
}

int query(int L,int R,int l,int r, int rt){//[L,R]是要查询的区间
    cout<<__func__<<" ["<<L<<','<<R<<"] ("<<l<<','<<r<<") "<<rt<<'\n';
    if(L<=l&&R>=r){//如果[L,R]里有(l,r)区间，直接返回对应的根节点
        return tree[rt];
    }
    pushDown(rt,len);
    int m = (l+r)>>1;
    int sum = 0;
    if(L<=m){
        sum += query(L,R,l,m,lson);
    }
    if(R>=m+1){
        sum += query(L,R,m+1,r,rson);
    }
    return sum;
}

int main(){
    build(1,vt.size(),1);
    showVtwithIndex(tree);

    update(3,6,10,1,7,1);//3到6全加10
    showVtwithIndex(tree);

    cout << query(3,5,1,7,1)<<'\n';
    showVtwithIndex(tree);
    return 0;
}
License

Adopting CC BY-NC-SA 4.0 License Agreement

Share

快来参与讨论吧~