3 无重复字符的最长子串
垃圾的滑动窗口:
外层 i, 内层 j 从 i 开始一点点加。结束内层后清理掉整个map 记忆的数据。
实际上不需要完全清理,只需要 i++ 后清理掉 i, j 可以继续++
4
1 | func getK(x, y []int, k int) float64 { |
5 最长回文子串
注意扩散法的解法,比 dp 更快
24 两两交换链表中的节点
写出来的太顺利了。还是二刷一下吧。
25 K 个一组翻转链表
25 也秒了,那我就不用重刷 24 了,有空重刷 25 吧。我可能是真会。
31
按照下面这个作者的思路,找到 i、j、k 三个数。即可。
i: 小数,从后往前第一个『有大哥』的数
j: i 后面,离 i 最近的大于 i 的
k: 大数。也是 i 后面,离 i 最远的大于 i 的
作者:Imageslr
链接:https://leetcode.cn/problems/next-permutation/solutions/80560/xia-yi-ge-pai-lie-suan-fa-xiang-jie-si-lu-tui-dao-/
标准的 “下一个排列” 算法可以描述为:
- 从后向前 查找第一个 相邻升序 的元素对 (i,j),满足 A[i] < A[j]。此时 [j,end) 必然是降序
- 在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
- 将 A[i] 与 A[k] 交换
- 可以断定这时 [j,end) 必然是降序,逆置 [j,end),使其升序
- 如果在步骤 1 找不到符合的相邻元素对,说明当前 [begin,end) 为一个降序顺序,则直接跳到步骤 4
按照这个思路的答案:
1 | func nextPermutation(nums []int) { |
34
我是自己手撸的查找。
看答案发现 golang 标准库里有个
1 | // SearchInts searches for x in a sorted slice of ints and returns the index |
找 x 放在有序数组a里的插入位置,
所以本题中左边界就是这个返回值,右边界呢只需要传 x+1 进去,就是我插入一个比 target 大的值的下标。再-1就是 target 的边界了。
39
很容易就可以写出不剪枝的答案版本。
看一种输入,2 3 7 ,target = 7 ,如果不能很好滴剪枝,就会导致两种情况
- 7=4+3 ,其实 7=3+4 重复,这个情况好减,只需要保证前面的数比后面的小(保留二组)或大(保留第一组)
- 2 2 3 和 3 2 2 重复,其实一个是 2+5 得到,一个是 3+4 得到,但这个怎么减呢?
从答案中去剪枝就麻烦了,除非再做一轮排序。根据答案,可以在搜索的时候就进行剪枝。
也就是说,用2开头的时候,我们可以用 [2 3 7] 来找剩下的答案。
所以在找 5 的时候可以找到 输入 237 找 5 , 第一个遍历2,找3,输入237找3,找到了返回上一层。
这时候找5回到3开头,就不要再输入 237找2了,而是输入37找2。
同理回到找7,刚刚用2找5,现在遍历3找4,就是 37找4, 自然是找不到 322这种情况,完成了剪枝。
41
两种方法,都需要重刷
45 跳跃游戏 II
虽然自己可以做出。但是可以看看特殊思路的解法开阔思路:
1 | func jump(nums []int) int { |
总结来说就是:我最多走多远?如果现在走到了曾经的最远。则说明我走到了更远的地方。需要再多走一步!
48 旋转图像
四个坐标的旋转关系其实还不麻烦,只要写出来一个 demo,对着就可以写出来他们的加减关系
反倒是这里有个细节就是 j 的遍历终点。
需要借助一张图去理解:
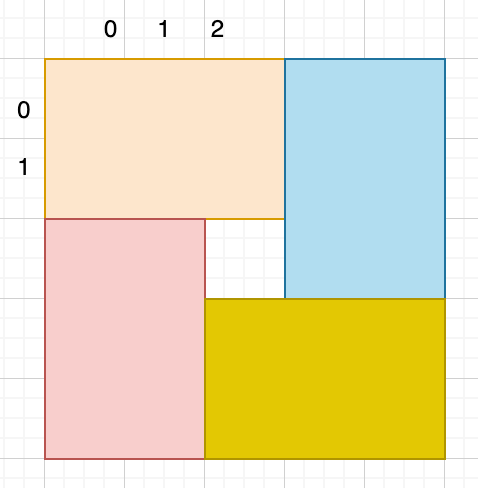
这里可以发现,在 5x5 的情况下,i的范围选[0,1],而 j 要选 [0,1,2]
所以i 很好处理,5/2 = 2,保证 i<2即可
而 j 要保证 j<3, 3是 (5+1)/2 还是 5/2+1 呢?
可以再用一个 4x4 的想一想,j 可以选 0,1
(4+1)/2 = 2
4/2+1 = 3 被排除
49 字母异位词分组
我用排序后的字符串作为 map 的 key
但是没想到,Go 的 map 可以用数组作为 key,而且可以自动判断数组元素是不是相等。详见:
1 | func TestMapKeyArray(t *testing.T) { |
这样就不需要排序了。统计字符出现次数就能判断是一组。
53 最大子数组和
动态规划很简单做了。分治法更为精妙,没试`
72 编辑距离
最开始我犯了一个错误,把 dp 公式在 word1[i-1] 和 word2[j-1] 一样的时候,dp[i][j] 的计算公式也当成了是取上方、左方和左上方的最小值。
会导致什么情况呢?
其实也很难发现,就是会导致字母一样切连续出现的时候。比如 o 和 ooo , 编辑距离应该是 2,但如果只是看 o 和 第二个的每个 o 比,都相同,那都取左上方的最小,就成了 0 了!完全错了。
实际上当他们一样的时候,编辑距离应该就等于它左上方的值。
从含义上理解就是:最后一个字母一样,代表可以不考虑这个字母,直接看两个单词都去掉这个字母的情况。
74 搜索二维矩阵
这里可以看下 Go 的 sort 包提供的二分查找方法:
1 | // This example demonstrates searching a list sorted in ascending order. |
更神奇的是,这个方法还可以用来做这题。后面可以再刷一下。其实是用了把二维转一维的思路。
75
其实是三指针
76 最小覆盖子串
不错。用了一个 map 也做出来了
78
我的递归太垃圾了。需要重刷。
84
二刷用单调栈做出来了。但是看答案还有个技巧,就是在切片的前后都补一个 0,就不需要特殊处理最后遍历完栈里还有数据的情况了。
101 对称二叉树
递归法和遍历法都要重刷
114 二叉树展开为链表
自己写出了递归法。但是可以实现O1的空间复杂度。
那就是【寻找前驱节点】法。
每次都是找当前节点 cur 的 Left 的最右下节点x,找到后
1 | x.Right = cur.Right |
122. 买卖股票的最佳时机 II
这题有一点很有意思。
他每天的动作必须是买或者卖。没说持有。他说的是:可以当天卖了再买。
其实卖了再买不就是持有吗!
但是你按照持有的思路去解题,就很难理解“暴力”的贪心解法。
你按照当天卖了再买的思路去想,其实就是每天和前一天比一下。如果赚钱就加入(等于昨天买了)。如果不赚钱就不加(昨天买了还是卖了我都不管,就当没有今天)。
123
有空刷一下吧
124
关键在于这个辅助函数的写法
1 | // 题目里算的结果可包含root也可不包含root |
首先是要不要返回值?因为其实这题的答案 ans 是在计算的过程中去更新的。
但是还是需要返回值,因为计算 root 的结果,需要传入root.L 和 root.R 拿到这两个返回值。
那么返回值要返回什么呢?
开始我错误地写成了,返回 root+L+R 的最大值。实际上是不行的。这样变成了求“和最大的子树”
因为本题是不允许路径有”往返”的情况的。所以只能返回root或 root+L 或 root+R。
而root+L+R的值虽然没有被返回,但是却在我们计算的过程中,计算出了结果sum,并判断这个结果目前是不是最大来更新我们最终的答案。
128
这题我第一次做自己用了比较麻烦的计算方法去算。
第二次用了暴力。但是没想到这个剪枝条件导致超时:
1 | if m[k-1] { |
其实就是,如果k-1存在,就不需要用 k 当做起点去找最长。直接跳过即可。
142 环形链表 II
主要是推算 a b c 三部分关系吧。下面是我的分析:
a 是环外长度。把环分成 b+c, b 是 fast 和 slow 相遇的位置距离入环点的距离,c 是剩下的距离
1 | 慢 = a + n圈(b+c) + 多走的 b |
所以
1 | 2a + 2n(b+c) + 2b = a + m(b+c) + b |
所以
1 | a + (2n-m)(b+c) + b = 0 |
就是说走 a 步 就等于 转 x 圈再倒退 b 步
我们让slow针转 x 圈,slow 还在当前点。我们让 slow 针再倒退 b 步,slow 所在的位置应该正好是入环点。
所以,从头开始走a步 == slow 走到入环点(a 步)
我们不知道 a 步是多少步,只能知道 slow 走 a 步后到的点 就是 你从头走a 步到的点。
也就是说判断两个指针是不是相遇,相遇了就是答案了。
146 LRU
注意技巧:伪头尾
160 相交链表
我用了遍历两边的方法。第一遍找出来长的,先走出长的距离。也是 O(m+n) 空间 O1 的
不过看了答案里的方法,更巧妙。代码更简单。
207 课程表
拓扑序列。直接贴个答案。很好理解。
1 | func canFinish(numCourses int, prerequisites [][]int) bool { |
215 数组中第 K 个最大元素
我想到了用快速排序的方法。但是我用的是最传统的快排,每次都是给 a[0] 挪到合适的位置。
这个解法能解小问题,但是当输入变成超长,且都是重复数字时,来回的挪位置会导致算法退化成 oN^2
看题解后发现,原来只需要确实位置,不需要去挪动 a[0]。这样做还可以不处理和 a[0] 相等的值。(只需要从左边找比a[0]大的,右边找一个比a[0]小的,然后交换,相等的不用管,因为不需要让数组变得有序,只需要知道a[0]应该去哪。
这里其实不好形容。我一会儿直接贴一下答案。
1 | func quick(nums []int, i, j int) int { |
题解里发现的时间最快的解法:
注意这个解法,不是通用的 TopK 解法,而是在本题已知所有元素范围都属于 [a,b] 后,然后在这个数据范围里去二分枚举,识图撞到正确答案。
1 | func init() { |
再说一下这题的堆法:要用大根堆。这里和求前 k 个元素还不一样。
- 求第 k 个,完全新建一个大根堆。然后pop 出 k-1个,堆顶的就是第 k 大的元素
- 求前 k 个,可以用上面的大根堆,在 pop 的过程中把 pop 出来的元素存入答案。但这样需要先完全建立一个大根堆。比较浪费。更好的方法是依次建立小根堆。发现堆的数量已经 k 个了。就开始判断堆顶。如果堆顶小于当前元素就弹出(必定不属于 topK)。最后堆里的元素就是 topK
238
有更优的解法,空间复杂度O(1),记得重刷
279
用四平方和定理,这就是一道简单数学题了
不用的话。我用了 dp ,也还好。
343 整数拆分
这题是数论了。拆出来的3越多越大
416
这种输入:[99 97 + 好多个100]
这种怎么剪枝呢?一直递归找,超时了。
使用了 map,存储从 i 开始找 target 是否能成功。如果找过就不再找了。
这里还需要注意。我的辅助函数 find 本来是 fund(a []int, target), 每次传入数组时传入a[i+1:],但实测这样会出现意想不到的问题。最后改成 find(i,target int),每次传入 i+1 代表从 i+1 开始找。这样问题更少。
答案用的 dp
437 路径总和 3
我想出了遍历的算法。没有想到更好的算法。
518
开始我的内外层循环搞错了,想的是:
用 ans[i] 存 i 的结果,然后一层层算上去。
这样会导致很多组合方法会被重复计算次数。
1 | for _, x := range coins { |
581 最短无连续子数组
这题关键是一个寻找思路,用白话形容是这样的:
我们先照着最大值为衡量去找。从左到右。
如果找到了一个比最大值还小的,那这个数必然得挪!
(比最大的max还大的 MAX,那不用挪MAX的,因为你是从左到右找到,在右边找到了MAX,只需要更新max=MAX,MAX它位置没毛病。 但是你继续往下找找到了比MAX 小的那就有问题了,你比我小怎么能在我右边呢?)
同理,可以从右向左,按照最小值为标准找更小的。
关于一种特殊情况,就是原来有序的,左右边界其实都不会被更新:
1 | if ansJ == ansI { |