Union-Find 算法详解
并查集算法,主要是解决图论中「动态连通性」问题的。名词很高端,其实特别好理解,等会解释,另外这个算法的应用都非常有趣。
先解释一下什么叫动态连通性吧。
一、问题介绍
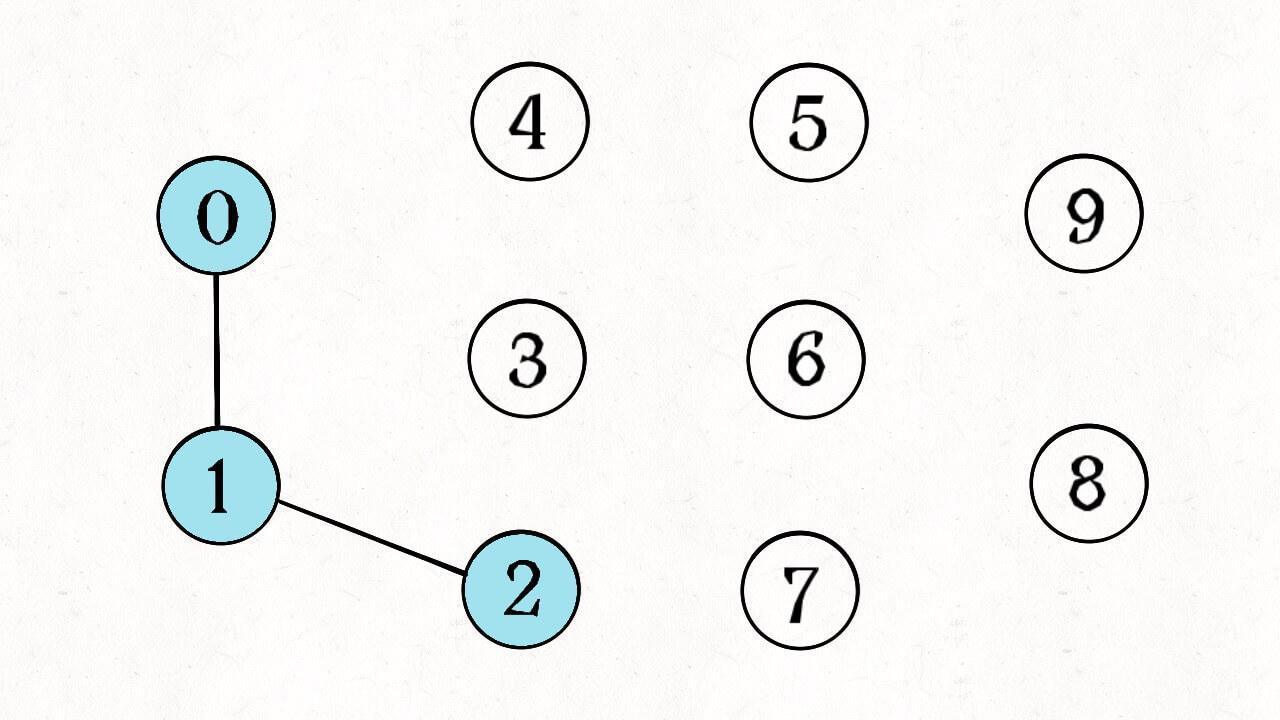
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:

现在我们的 Union-Find 算法主要需要实现这两个 API:
1 | class UF { |
这里所说的「连通」是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
比如说之前那幅图,0~9 任意两个不同的点都不连通,调用 connected 都会返回 false,连通分量为 10 个。
如果现在调用 union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。
再调用 union(1, 2),这时 0,1,2 都被连通,调用 connected(0, 2) 也会返回 true,连通分量变为 8 个。
判断这种「等价关系」非常实用,比如说编译器判断同一个变量的不同引用,比如社交网络中的朋友圈计算等等。
这样,你应该大概明白什么是动态连通性了,Union-Find 算法的关键就在于 union 和 connected 函数的效率。那么用什么模型来表示这幅图的连通状态呢?用什么数据结构来实现代码呢?
二、基本思路
注意我刚才把「模型」和具体的「数据结构」分开说,这么做是有原因的。因为我们使用森林(若干棵树)来表示图的动态连通性,用数组来具体实现这个森林。
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:
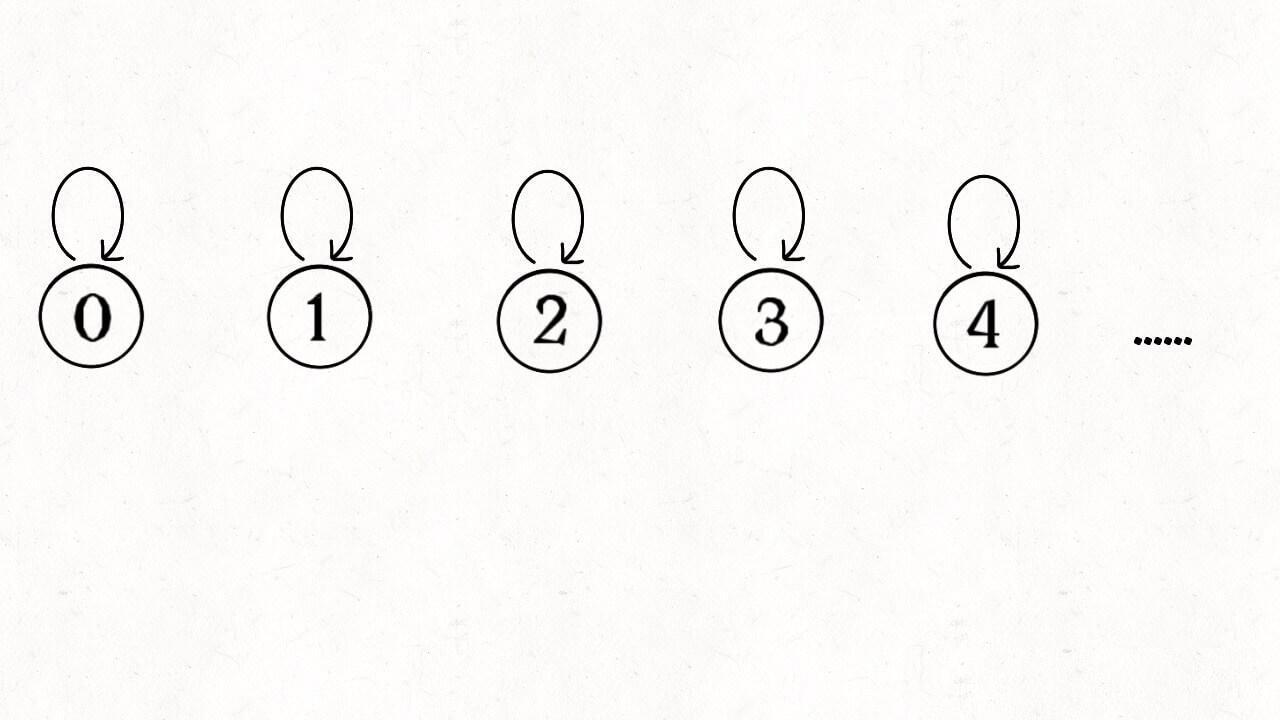
1 | class UF { |
如果某两个节点被连通,则让其中的(任意)一个节点的根节点接到另一个节点的根节点上:
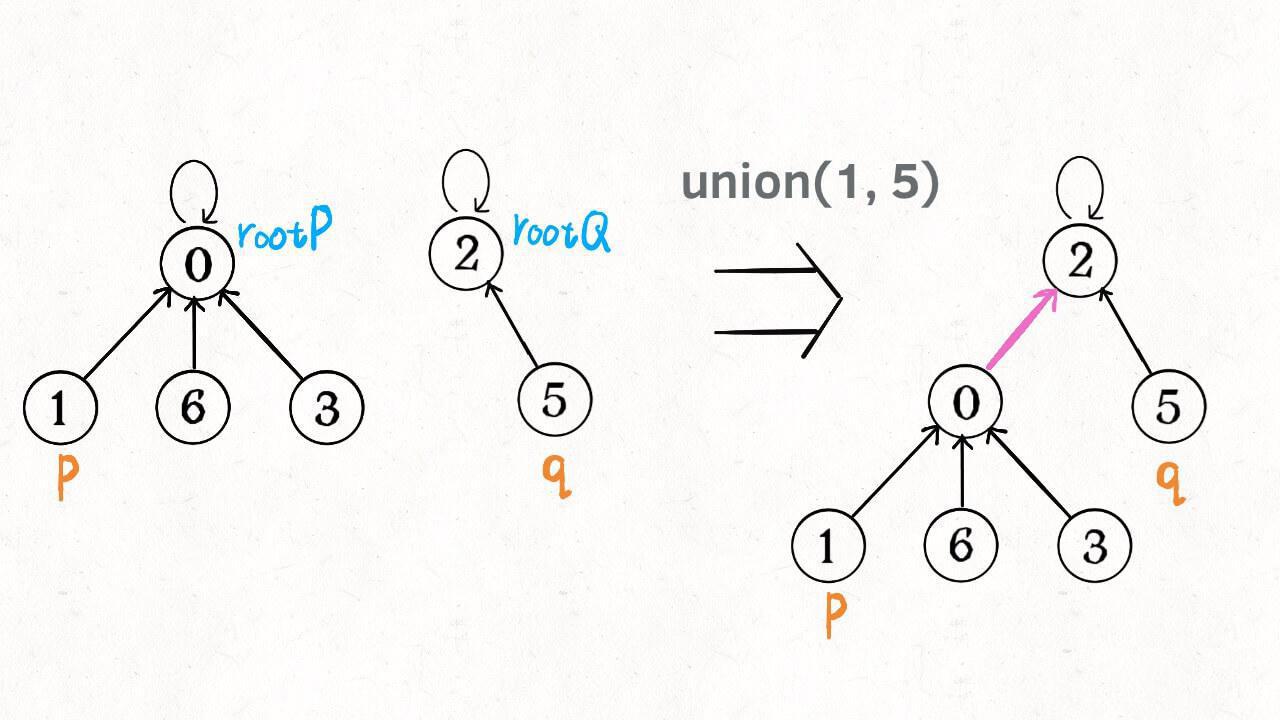
1 | public void union(int p, int q) { |
这样,如果节点 **p** 和 **q** 连通的话,它们一定拥有相同的根节点:
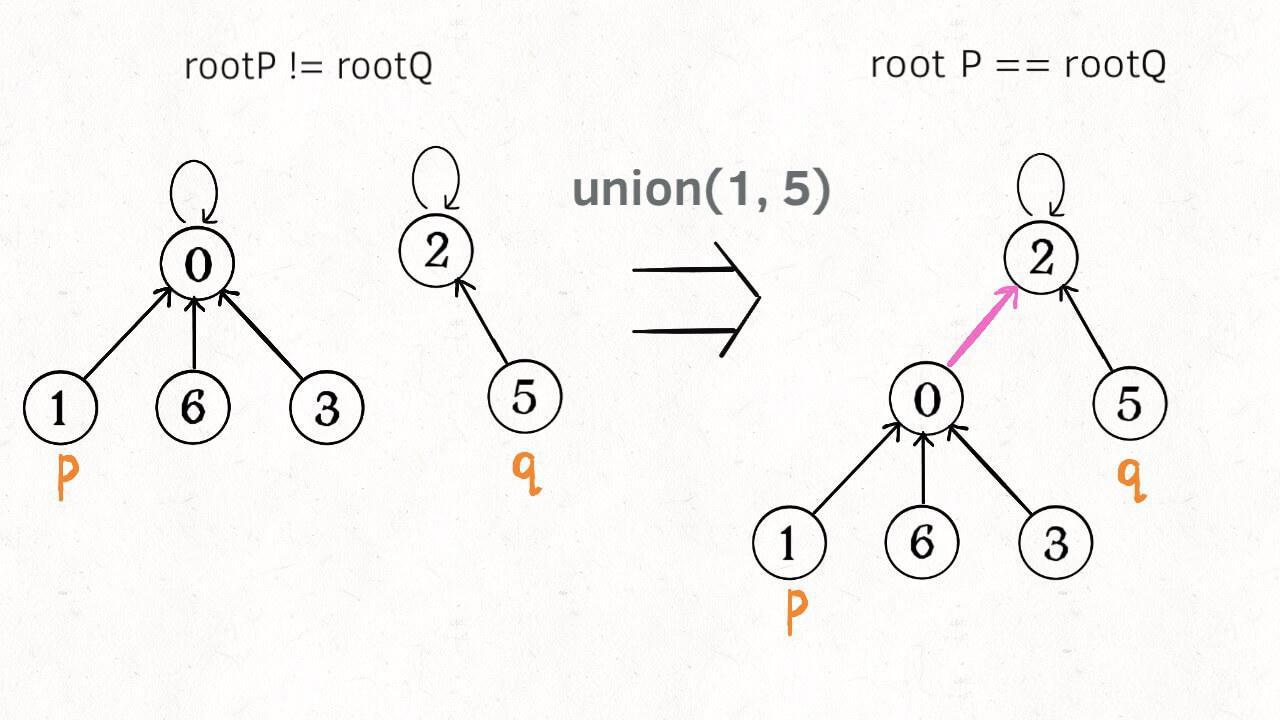
1 | public boolean connected(int p, int q) { |
至此,Union-Find 算法就基本完成了。是不是很神奇?竟然可以这样使用数组来模拟出一个森林,如此巧妙的解决这个比较复杂的问题!
那么这个算法的复杂度是多少呢?我们发现,主要 API connected 和 union 中的复杂度都是 find 函数造成的,所以说它们的复杂度和 find 一样。
find 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN,但这并不一定。logN 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 N。
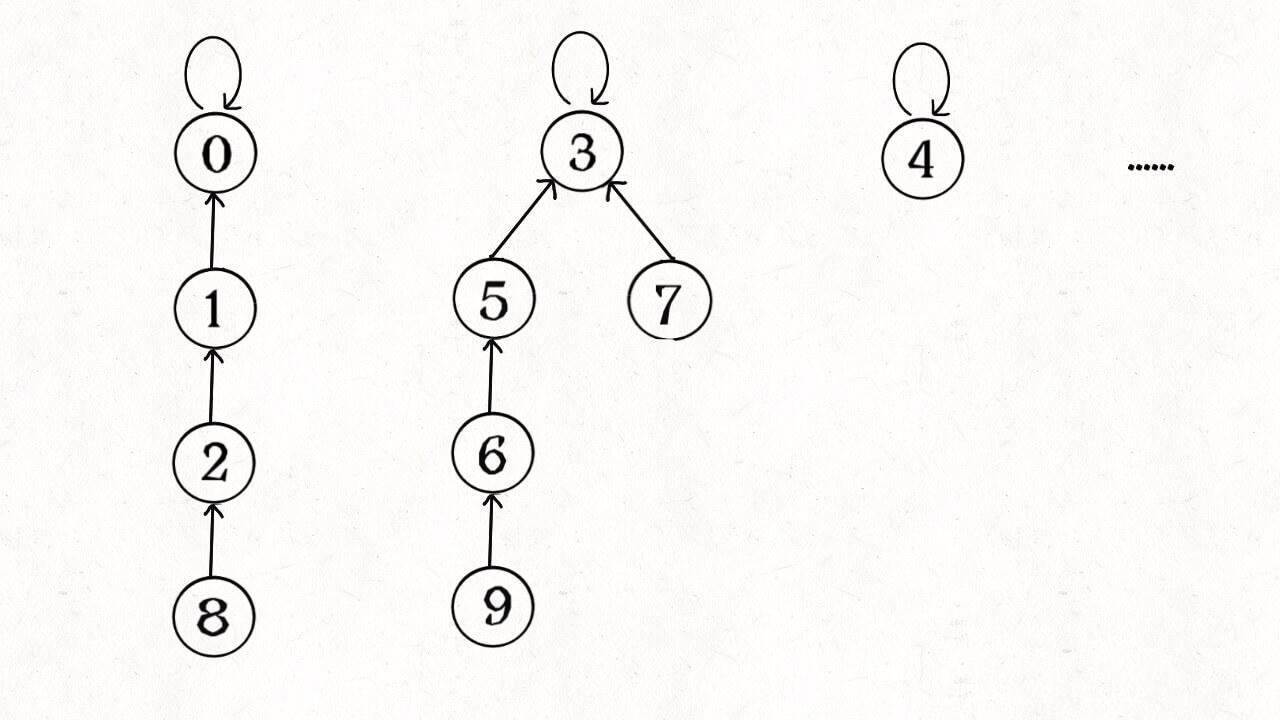
所以说上面这种解法,find , union , connected 的时间复杂度都是 O(N)。这个复杂度很不理想的,你想图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 union 和 connected 的调用非常频繁,每次调用需要线性时间完全不可忍受。
问题的关键在于,如何想办法避免树的不平衡呢?只需要略施小计即可。
三、平衡性优化
我们要知道哪种情况下可能出现不平衡现象,关键在于 union 过程:
1 | public void union(int p, int q) { |
我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:
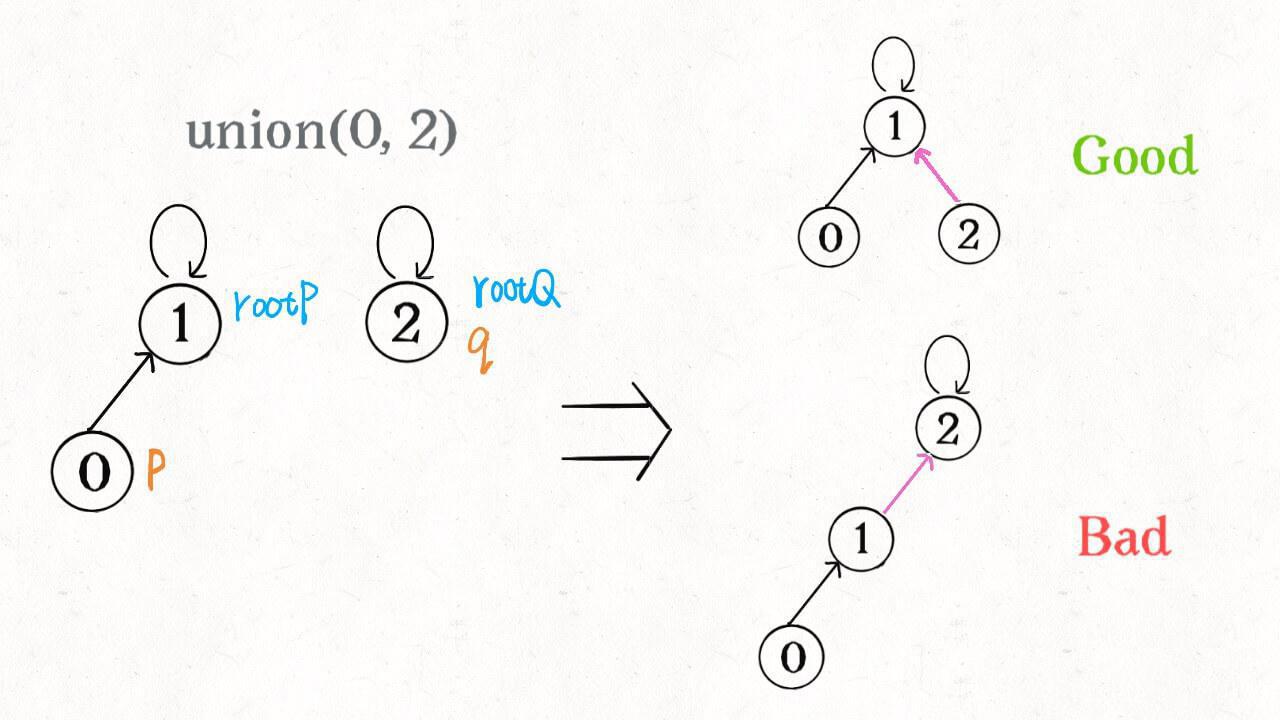
长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个 size 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
1 | class UF { |
比如说 size[3] = 5 表示,以节点 3 为根的那棵树,总共有 5 个节点。这样我们可以修改一下 union 方法:
1 | public void union(int p, int q) { |
这样,通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级,极大提升执行效率。
此时,find , union , connected 的时间复杂度都下降为 O(logN),即便数据规模上亿,所需时间也非常少。
四、路径压缩
这步优化特别简单,所以非常巧妙。我们能不能进一步压缩每棵树的高度,使树高始终保持为常数?
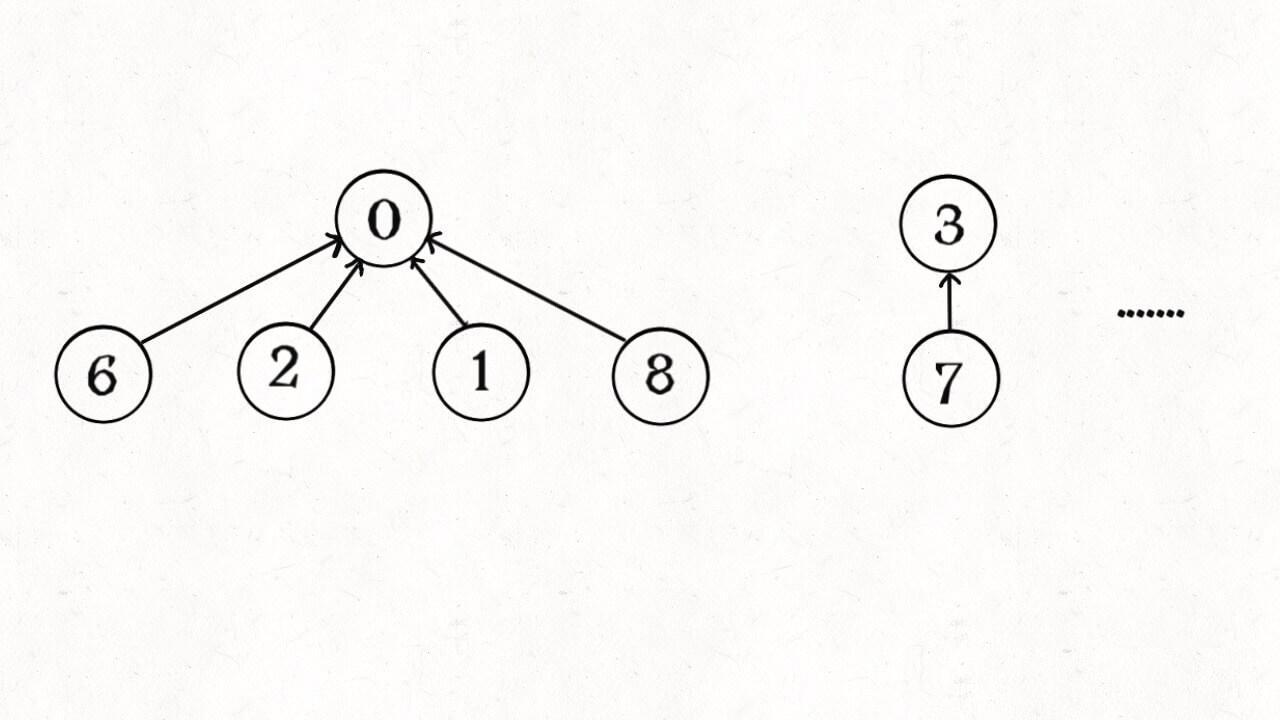
这样 find 就能以 O(1) 的时间找到某一节点的根节点,相应的,connected 和 union 复杂度都下降为 O(1)。
要做到这一点,非常简单,只需要在 find 中加一行代码:
1 | private int find(int x) { |
这个操作有点匪夷所思,看个 GIF 就明白它的作用了(为清晰起见,这棵树比较极端):
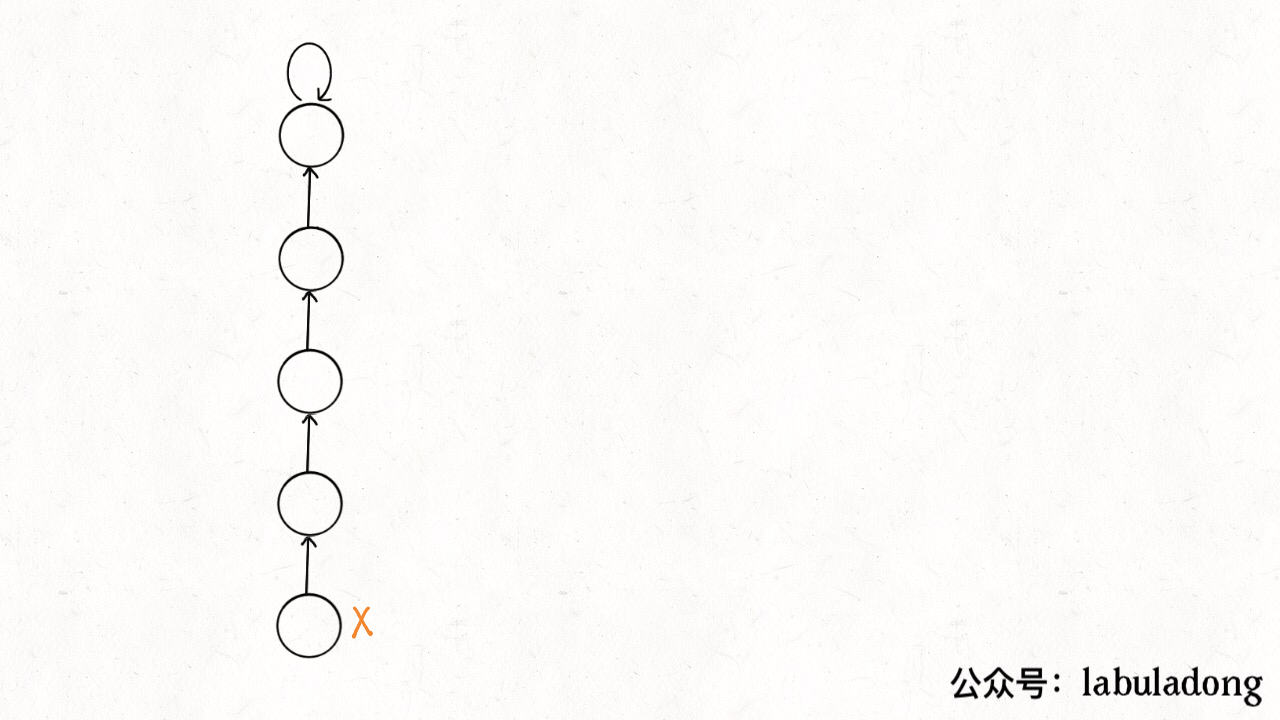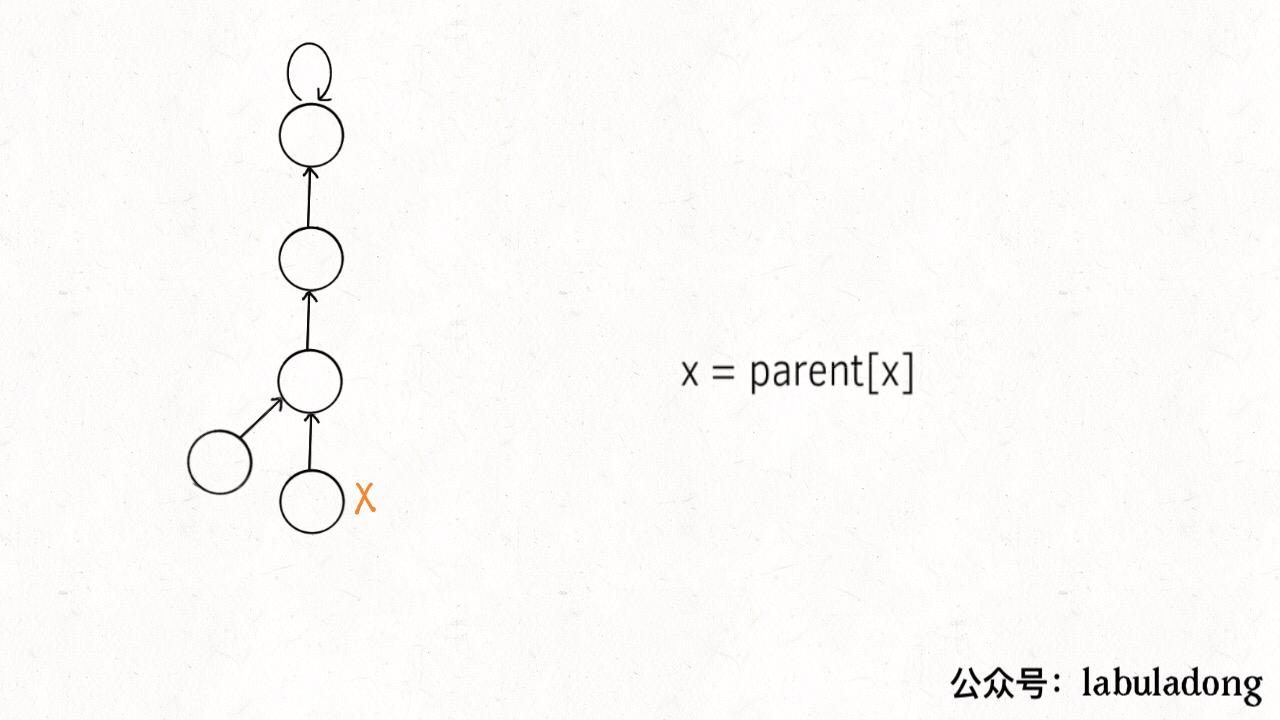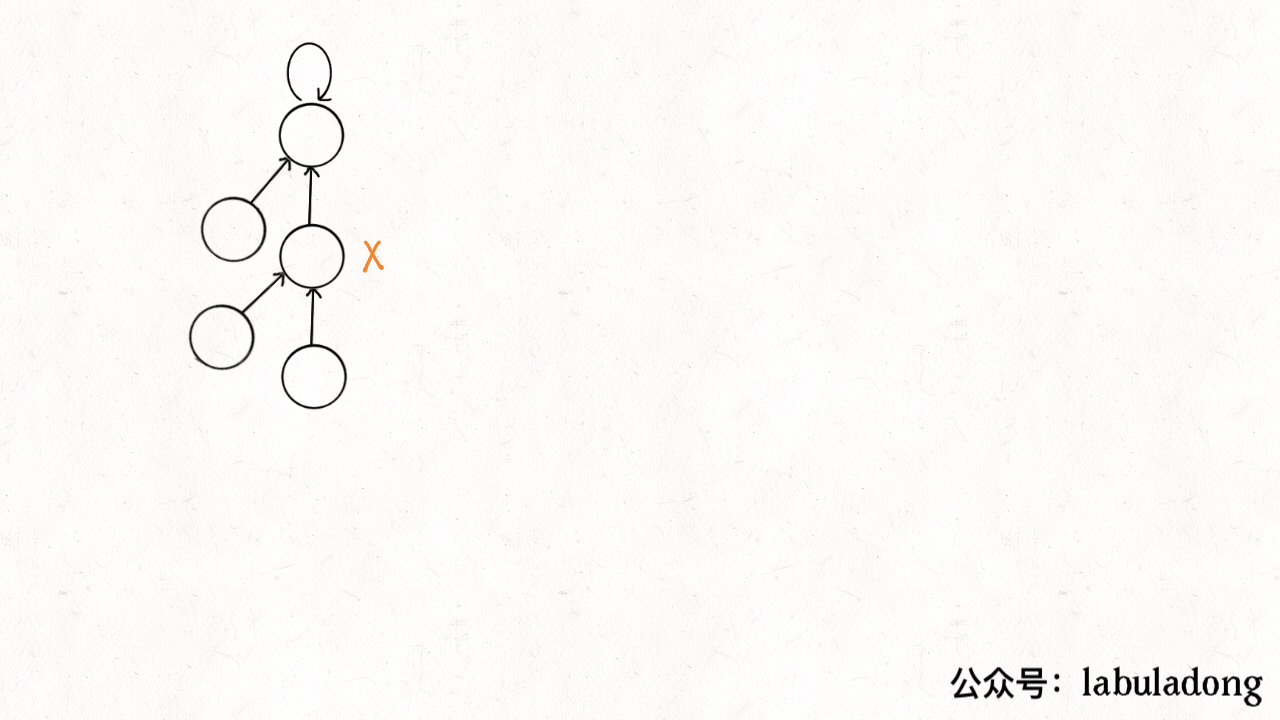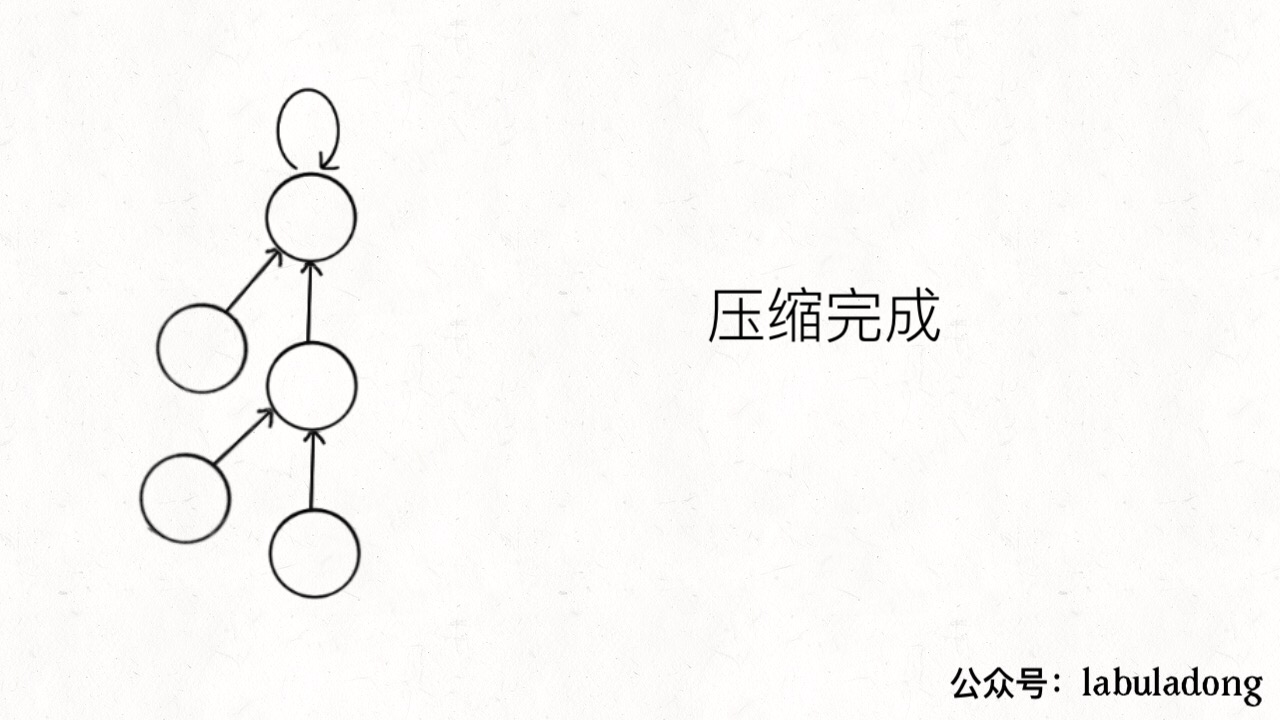
可见,调用 find 函数每次向树根遍历的同时,顺手将树高缩短了,最终所有树高都不会超过 3(union 的时候树高可能达到 3)。
PS:读者可能会问,这个 GIF 图的find过程完成之后,树高恰好等于 3 了,但是如果更高的树,压缩后高度依然会大于 3 呀?不能这么想。这个 GIF 的情景是我编出来方便大家理解路径压缩的,但是实际中,每次find都会进行路径压缩,所以树本来就不可能增长到这么高,你的这种担心应该是多余的。
五、最后总结
我们先来看一下完整代码:
1 | class UF { |
Union-Find 算法的复杂度可以这样分析:构造函数初始化数据结构需要 O(N) 的时间和空间复杂度;连通两个节点 union、判断两个节点的连通性 connected、计算连通分量 count 所需的时间复杂度均为 O(1)。
好了,本文就讲到这里,相信你已经掌握了 Union-Find 算法的核心逻辑。
练习
提示:这道题核心思想是,将 **equations** 中的算式根据 **==** 和 **!=** 分成两部分,先处理 **==** 算式,使得他们通过相等关系各自形成连通分量;然后处理 **!=** 算式,检查不等关系是否破坏了相等关系的连通性。
实战总结
自己写 UF 的时候有以下两点需要注意
- 找x的父亲的时候,其实不是直接返回 m[x],而是要一直找 m[x] 直到 m[x] == x,这样才能保证找对了
- 连接的时候也是。连 x 和 y,其实是连 x 的父亲和 y的父亲
我自己写时疏忽了上面的点,导致一些错误的 case